因明とは?
「因明」とは仏教の論理学です。
インドの瑜伽行派の僧侶・ディグナーガ(陳那)が体系化しました。
それが素晴らしかったために、仏教の内外で使われる論争の共通のルールとなり、インド哲学に大きな影響を与えました。
中国や日本では、法相宗で重視され、研究されています。
心の仕組みを精密に解明した唯識を学ぶのに必要となります。
因明は大変難解だとされますが、一体どんな論理なのでしょうか?
因明とは
まず、因明について、仏教の辞書を参照しておきましょう。
以下のように出ています。
因明
いんみょう[s:hetu-vidyā]声明・工巧明・医方明・内明と並ぶ、インド古来の五明(五つの学問)の一つ。
論理学。
文字通りの意味からすれば、推理・推論における理由(因)(hetu)についての学問ということになるが、本来は、議論の技術・規則を考察する学問であった。
インドの王侯たちは、古くから異なった諸宗教・諸哲学の間の論争の集会(日本でいえば宗論に近い)を目の前で行わせ、その優劣を見極め、議論に勝利をおさめたほうに財政的援助を厚くするという風習があったため、因明は一種の死活問題であり、それだけ熱心に研究された。西暦5-6世紀頃に現れたディグナーガ(陳那)は、それまでの議論の技術というよりも、推理・推論そのものに論究の焦点を当て、<因>の正しいありかた、正しくないありかたを明らかにし、通常いう<論理学>に匹敵する学問を確立した。
そのため、ディグナーガよりも前の因明は<古因明>、それ以降の因明は<新因明>と呼ばれるようになった。
新因明は、ニヤーヤ学派との論争を経ながら、ダルマキールティ(法称)などによって精緻な体系が築かれた。
ただ、漢訳され、とくに注目されたのは、ディグナーガの『因明正理門論』、およびディグナーガとほぼ同時期のシャンカラスヴァーミン(商羯羅主)作とされる『因明入正理論』という綱要書であった。
とりわけ後者には、基による『因明入正理論疏』(別称『因明大疏』)という膨大な注釈書が書かれ、日本では、因明の研究といえば、もっぱらこの注釈書の研究を指した。奈良時代の秋篠寺の善珠を始めとして、因明の学者は連綿と現れ、とくに法相宗においてその伝統は重視された。
平安期まで天台宗でも因明を重視し、因明に従った論義がなされていたが、後には天台宗で用いなくなった。(引用:『岩波仏教辞典』第三版)
このように、「因明」の「因」というのはインドの言葉でへートゥ(hetu)ということで、原因のことです。
自分の主張に至る理由を表しています。
「因明」の「明」はインドの言葉でヴィデャーということで、学問のことです。
つまり因明とは、主張の理由としてどんなものが適切かを明らかにする学問という意味で、論理学のようなものです。
ですがこの辞書だと、あとは因明の内容というよりも、因明の歴史を説明していますので、以下で因明の内容について分かりやすく解説します。
ディグナーガまでの論理学「古因明」
インドでは昔から色々な思想が現れ、論争が行われてきました。
ですが、論争する時には、双方に共通のルールがなければ、勝敗が決まりません。
その論争の共通ルールが古くから研究されてきました。
伝統的なインド哲学六派の中でも、ニヤーヤ学派では論理学を専門に研究したとされています。
ニヤーヤ学派の開祖のガウタマは、1世紀頃の人で、ニヤーヤ学派の聖典である『ニヤーヤ・スートラ』を書いたとされますが、内容的には3世紀から4世紀に現在に伝わる形になったものといわれています。
このような、ディグナーガまでの因明を古因明といいますが、古因明についての現存する最古の文献は1〜2世紀に成立した『チャラカ本集』です。
これは、チャラカという医師の書いた医学書といわれますが、その中に因明について論じられています。
そこには、自分の主張を論証する作法を5つのステップで定式化されています。
これを「五分作法」といいます。
5ステップで主張を正当化する「五分作法」
五分作法の論証のステップはどんなものかというと、宗、因、喩、合、結の5つです。
1つ目の「宗」とは主張のことです。
自分が論証したい命題です。
2つ目の「因」とは理由のことです。
その主張を正当化する根拠です。
3つ目の「喩」とは、実例です。
因だけだとまだよく分からないので、因を実証する実例を1つ挙げます。
4つ目の「合」は、適合させることです。
実例と同じことが最初に挙げた主張にも言えるということです。
5つ目の「結」は、結論です。
基本的に自分の主張である「宗」の繰り返しになります。
これは『ニヤーヤ・スートラ』にも出ているスタンダードな論証のステップです。
具体例を挙げるとこうなります。
1.「宗」……言葉は無常である。
2.「因」……なぜなら作られたものだから
3.「喩」……例えば壺のように作られたものは無常である。
4.「合」……壺と同じように言葉も作られたものである。
5.「結」……故に言葉は無常である。
五分作法の問題点
これが五分作法ですが、納得できるでしょうか?
小中学校で数学の証明を習った現代人にとって、これで本当に論証したといえるのか疑問が起きると思います。
もちろん因明は西洋の論理とは異なるものですが、それでも作られた壺が無常だと、どうして作られた言葉が無常だといえるのかは不明瞭です。
このように古因明は、共通の性質を持つ別の一例から類推して、自分が言わんとするものも同じだと主張するものです。
つまり、たとえ話みたいなものです。
たとえなので、必ずしもそうとは言えない可能性があり、いかに誰もが納得する分かりやすい実例を挙げられるかが、説得力を高める上での重要ポイントになります。
どちらかといえば、現代でも説得力のある話の順序として定式化されているPREP法のようなものです。
PREP法は、以下の順番で話を構成します。
1.POINT、要点・結論です。
2.REASON、理由です。
3.EXAMPLE、例です。様々な事例やデータを出します。
4.POINT、もう一度要点・結論です。
これらの頭文字を集めると、PREPになるわけです。
これは、古因明の「合」は省略してありますが当然のことなので、本質的に古因明と同じであることが分かると思います。
ですから、古因明は、因明とはいわれますが、論理というよりも説得術のようなものだったのです。
そんな中で、どんな理由なら確実な主張の根拠になるかを明らかにし、説得術を論理の領域まで高めたのがディグナーガの新因明です。
ディグナーガの「新因明」
ディグナーガとは
ディグナーガというのは、480年頃から540年頃の人です。
ディグを陳、ナーガを那と音訳して陳那といわれます。
最初は小乗仏教の犢子部で出家しましたが、大乗仏教に転向して世親菩薩に唯識を学んだといわれる瑜伽行派の僧侶です。
主著は『集量論(プラマーナサムッチャヤ)』です。
その中で新因明を打ち立て、仏教にも、それ以外の人々にも大きな影響を与えました。
3ステップで論証する「三支作法」
新因明では、論証式のステップが宗、因、喩の3つになります。
まず、古因明(五分作法)の「結」は「宗」と同じなので省略されています。
そして、古因明にあった「合」は、次の因の性質を明らかにされた「因の三相」によって、因の性質に含まれてしまいます。
従って、宗、因、喩の三支作法が新因明の論証のステップとなります。
3ステップなのは、西洋の三段論法と同じです。
三段論法はこのような3ステップです。
1.「大前提」……人間は死すべきものである。
2.「小前提」……ソクラテスは人間である。
3.「結論」……ソクラテスは死すべきものである。
このように三段論法は、理由を先にいって結論を導きます。
ですが因明ではそれと逆に、結論を先に言って、理由を述べます。
具体的には、以下のようになります。
1.「宗」(主張)……言葉は無常である
2.「因」(理由)……すべての作られたものは無常であるから
3.「喩」(実例)……例えば壺のように作られたものは無常である。逆に常住なものは虚空のように作られたものではない。
具体例を分かりやすいようにソクラテスでそろえると、こうです。
1.「宗」……ソクラテスは死すべきものである。
2.「因」……すべての人間は死すべきものであるから。
3.「喩」……例えば歴史の教科書に出てきた人たちのように、人間は死すべきものである。逆に死なないものは、おばけのように、人間ではない。
これで論証完了です。
この新因明が成立するためには、2番目のステップの因について、満たさなければならない条件が3つあるといいます。
それが「因の三相」です。
因の三相(適切な理由の持つ3つの性質)
一応読み方は、「いんのさんぞう」と読みます。
因の三相は、誰が初めに言ったのかは分かりません。
世親菩薩の実兄の無著菩薩の著作にも出てきます。
ですが、それは無著菩薩の相手が使っているものです。
ディグナーガはその因の三相を正しい因の条件として明確にしています。
では因の三相とはどんなものかというと、「遍是宗法性」「同品定有性」「異品遍無性」の3つです。
1.遍是宗法性(主題の属性であること)
まず1つ目の「遍是宗法性」とは、主張である宗の主題(主語)に、因と同じ性質があるということです。
「遍是宗法性」自体は、遍くこれ宗が(因の)法である性質、という意味です。
先ほどの具体例の「言葉は無常である」という宗でいえば、宗の主題(主語)である「言葉」に、因として挙げられた、「作られたもの」という性質がある、ということです。
例えば、これを満たさないものとして、「原子でできているものは無常だから」を因とすると、言葉は原子でできているという性質を持たない(原子でできていない)ので、主張と無関係になります。
「ソクラテスは死すべきものである」という宗でいえば、主題(主語)である「ソクラテス」に、因としてあげられた「人間(は死すべきもの)だから」の、人間という性質がある、ということです。「ソクラテスは死すべきものである」と言いたいのに、なぜなら「ネコは死すべきものだから」と言っても、今、ソクラテスの話をしているのに、ソクラテスはネコではないから理由にならないということです。
主張と無関係な理由は因として不適切なので、主張の主題(主語)は、必ず因の性質を持たねばならないということです。
当たり前ですね。
ですがこれによって、五分作法の「合」はいらなくなります。
2.同品定有性(同品に存在すること)
次に2つ目の「同品定有性
」とは、同品に因に挙げた性質のあるものが存在するということです。
同品とは、主張である宗の述語を満たす集合です。
上記の「言葉は無常である」という具体例でいうと、同品は、宗の述語にある、無常であるものの集合です。
その同品の中に、因に挙げた「作られたもの」が存在するという条件が、「同品定有性」です。
三支作法の3番目の「喩」として具体例を挙げると、無常であるものの集合に、作られたものとして「壺」が存在します。
死すべきものの例であれば、人間として、歴史上の人物が存在します。
ですが、もしかしたら異品の中にも、「作られたもの」が存在するかもしれません。
そこで、次の3番目の条件に進みます。
3.異品遍無性(異品に存在しないこと)
最後に3つ目の「異品遍無性
」とは、異品に因に挙げた性質のものが存在しないという性質です。
「異品」とは、同品の補集合のことです。
この具体例でいえば無常ではないものの集合、
言葉を変えれば常住なるものの集合です。
その常住なるものの中には、因に挙げた、作られたものは存在しないという条件です。
ソクラテスの例なら、死なないものの中には、因にあげた「人間」は存在しない、ということです。
これが3番目の、異品遍無性です。
三支作法の「喩」として具体的に、常住なものの中に存在する「虚空」は作られたものではありません。
常住なものの中に、作られたものは存在しないのです。
この2つ目と3つ目の条件によって明らかになるのが、遍充関係です。
この遍充関係が重要です。
遍充関係(包含関係)
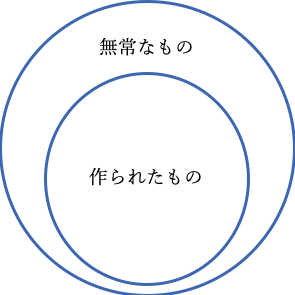
遍充関係
遍充関係というのは、包摂関係、つまり包含関係のことです。
作られたものならば、必ず無常であるとすれば、作られたものの集合は無常であるものの集合に含まれているか、或いは等しいことになります。
遍充とは包含のことなので、無常である集合が、作られたものの集合を遍充しているという言い方をします。
作られたものの集合は無常である集合に遍充されている、ということです。
因に挙げた性質の集合が、宗の述語の集合である同品に包まれているという関係です。
この遍充関係によって、作られたものは必ず無常だという関係にあるので、まるで三段論法のように結論である宗を論証することができます。
具体例でいえば、作られたものは必ず無常である。
言葉は作られたものである。
だから言葉は無常である、という具合です。
九句因(マトリックスによる確認)
この関係を明らかにするために、9つの場合を調べたのが九句因です。
これはディグナーガがオリジナルで考えたことです。
どんな9つの場合かというと、まず因の性質が、集合の要素すべてにある場合を有、一部にある場合を有非有、一切ない場合を非有とします。
すると、同品と異品について、それぞれ3通りの場合があるので、全部で9通りの場合があります。
表にするとこうなります。
| 異品有 | 異品非有 | 異品有非有 | |
|---|---|---|---|
| 同品有 | 第一句 | 第二句 | 第三句 |
| 同品非有 | 第四句 | 第五句 | 第六句 |
| 同品有非有 | 第七句 | 第八句 | 第九句 |
これを具体例つきで列挙すると以下のようになります。
第一句:同品有異品有:宗・言葉は常住:因・認識できるから:喩・虚空、壺
第二句:同品有異品非有:宗・言葉は無常:因・作られたものだから:喩・壺、虚空
第三句:同品有異品有非有:宗・言葉は努力の結果:因・無常だから:喩・壺、稲妻と虚空
第四句:同品非有異品有:宗・言葉は常住:因・作られたものだから:喩・虚空、壺
第五句:同品非有異品非有:宗・言葉は常住:因・聞こえるから:喩・虚空、壺
第六句:同品非有異品有非有:宗・言葉は常住:因・努力の結果だから:喩・虚空、壺と稲妻
第七句:同品有非有異品有:宗・言葉は努力の結果ではない:因・無常だから:喩・稲妻と虚空、壺
第八句:同品有非有異品非有:宗・言葉は無常:因・努力の結果だから:喩・壺と稲妻、虚空
第九句:同品有非有異品有非有:宗・言葉は常住:因・形を持たないから:喩・虚空と原子、運動と壺
理由にならない理由4種類
少し詳しく確認すると、第一句の具体例では、宗は言葉は常住である、ということです。
同品は常住である集合です。
その中に因の認識できるものは存在するかというと、常住であるもの全体が認識できます。
例えば虚空です。
では異品である無常である集合に、認識できるものは存在するかというと、こちらも無常なもの全体が認識できます。
例えば壺です。
この場合、言葉が認識できるからといって、常住だといえるかというと、認識できるもので無常なものがあるので、その理由で常住と結論することはできません。
このような因は不適切ということになります。
これと同じことは、第三句にも言えます。
宗は言葉は努力の結果であるということを結論したいとします。
同品である努力の結果である集合に、因である無常なものがあるかというと、全体がそうです。
例えば壺です。
では異品である努力の結果でない集合に無常なものはあるかというと、一部あります。
例えば稲妻です。
ですが、常住なものもあります。
例えば虚空のようなものです。
この場合、無常なものの中に、努力の結果もあればそうでないものもあるので、言葉が無常だからといって、努力の結果とは限りません。
因としては不適切ということになります。
同様に、第七句と第九句も、因の性質が、同品にも異品にもあるので、因として不適切です。
因の三相でいえば、2番目の同品定有性は満たしていますが、3番目の異品遍無性を満たしていないので、因としては不適切なのです。
論争している時にこのような因を出したら、「そんなの理由になりませんよ」と言われてしまいます。
意味不明な理由1種類
次に、第五句はどうでしょうか。
宗は言葉は常住ですから、そういう結論を導きたいとします。
同品である常住である集合に、因である聞こえるものはあるかというと、ありません。
例えば常住である虚空が聞こえないようなものです。
では異品である無常である集合に、聞こえるものがあるかというと、ありません。
例えば壺が聞こえないようなものです。
この場合、聞こえるというのは、言葉だけに特有の性質です。
このような因の三相の2番目も3番目も満たさない、そのものに特有の性質を理由に挙げても、結論を導くことはできません。
こんな理由を挙げても意味不明です。
ですから因としては不適切です。
これを論争で出したら、「何言ってんの?」と相手にされないことでしょう。
逆を論証してしまう理由2種類
次に第四句はどうでしょうか。
結論づけたい宗は言葉は常住ということです。
同品である常住な集合に、因である作られたものはあるかというと、ありません。
常住である虚空は作られたものではないようなものです。
では、異品である無常である集合に、作られたものはあるかというと、全体がそうです。
例えば壺のようなものです。
この場合、言葉は作られたものだから、最初に言いたかったことと反対の、言葉は無常であることを結論づけてしまいます。
これは因としては不適切です。
というよりも論争の時にこれを出したら、相手の勝ちになり、自分は敗北してしまいます。
それと同様に、第六句も同じです。
結論づけたい宗は、同じく言葉は常住であるということです。
同品である常住の集合に、努力の結果であるものはあるかというと、ありません。
常住である虚空が、努力の結果ではないようなものです。
では異品である無常である集合に、努力の結果であるものはあるかというと、一部あります。
無常である稲妻は努力の結果ではないですが、壺は努力の結果であるようなものです。
この場合、やはり努力の結果であるものは無常なので、言葉も無常ということになってしまいます。
これも逆に相手の主張を論証してしまう不適切な因です。
適切な理由2種類
では、第二句と第八句はどうでしょうか。
これは、どちらも結論づけたい宗は言葉は無常であることです。
同品である無常である集合に、第二句の理由の作られたものだからは全体が合致します。
第八区の努力の結果については、一部が存在します。
異品である常住の集合には、第二句の作られたものも、第八句の努力の結果であるものも存在しません。
この場合、作られたものだからといっても、努力の結果であるからといっても、結論を導くことができます。
因の三相を満足する、適切な因ということになります。
このように、九通りに分けて調べると、その中で、実に第二句と第八句の2つだけが、適切な理由になることが分かるのです。
ディグナーガの天才的な所
ディグナーガはさらに、因の三相の二番目と三番目を1つにまとめられるのではないかと考えました。
それは、「2.同品に因に挙げた性質のあるものが存在する」に「のみ」を入れて「同品にのみ因に挙げた性質のあるものが存在する」とします。
そして、「3.異品に因に挙げたものが存在しない」に「決して」を入れて「異品に因に挙げたものが決して存在しない」とすることです。
これで2と3が同じ意味になり、1つでよくなります。
さらにこれを確認すれば、九区因の9通りを確認しなくてもよくなります。
このように、論理学を大きく発展させたのが、ディグナーガの天才的なところです。
例示は2つ?
こうして、三支作法が以下のようになる明確な理由が明らかになりました。
1.「宗」……言葉は無常である
2.「因」……すべての作られたものは無常であるから
3.「喩」……例えば壺のように作られたものは無常である。逆に常住なものは虚空のように作られたものではない。
「喩」は因の三相の2番目と3番目、すなわち同品に実例が存在することと、異品には存在しないことを示すため、2つ挙げることになります。
では、たった2つでいいのでしょうか?
西洋のユークリッド幾何学の証明では、2つでは不十分です。
ですが、その場合、線には長さだけあって幅はないなど、現実には存在しない、理想的な世界での話です。
仏教で扱うのは、物理学と同じように、現実の世界です。
ですから、すべての例を調べ尽くすことは不可能です。
例えば「カラスは黒い」という時に、すべてのカラスを調べることはできないので、ある程度調べて結論します。
理想的な、いわば架空の世界を扱う時には演繹が可能ですが、現実を扱う時にはどうしても帰納的にならざるをえないのです。
それで、現実を扱っている仏教では、代表例を1つ挙げることによって、論証式を立てます。
幾何学だったらそれで証明終わりですが、この三支作法の論証式をあげても、それで証明されたわけではないので、そこからがスタートです。
その論証式が成り立つかどうかを対論者と確かめていきます。
そのやりとりの過程が論争なのです。
こうして、ディグナーガの因の三相を伴う三支作法は、それまでの五分作法とは次元の違う説得力を発揮したため、仏教以外の人々にも取り入れられ、当時の論理学のステージを大きく高めたのでした。
仏教には何が教えられている?
では、このようなすぐれた論理を使って、仏教ではどんなことを解明されているのでしょうか?
それは、仏教の目的とする、苦しみの根本的な解決です。
例えばディグナーガの論理学は、さらに孫弟子のダルマキールティ(法称)などによって発展していきますが、ダルマキールティなどは、輪廻を論証したりしています。
そのような、苦しみの根本解決を明らかにする手段として、仏教で論理学が発展したのです。
では、仏教では、苦しみの根本原因をどのようなものだと明らかにされ、どうすればそれを解決できると教えられているのでしょうか?
その苦しみの根本原因とその解決については、
仏教の真髄ですので、電子書籍とメール講座にまとめておきました。
ぜひ知っておいてください。
関連記事
この記事を書いた人

長南瑞生(日本仏教学院創設者・学院長)
東京大学教養学部で量子統計力学を学び、1999年に卒業後、学士入学して東大文学部インド哲学仏教学研究室に学ぶ。
25年間にわたる仏教教育実践を通じて現代人に分かりやすい仏教伝道方法を確立。2011年に日本仏教学院を創設し、仏教史上初のインターネット通信講座システムを開発。4,000人以上の受講者を指導。2015年、日本仏教アソシエーション株式会社を設立し、代表取締役に就任。2025年には南伝大蔵経無料公開プロジェクト主導。従来不可能だった技術革新を仏教界に導入したデジタル仏教教育のパイオニア。プロフィールの詳細・お問い合わせ
X(ツイッター)(@M_Osanami)、ユーチューブ(長南瑞生公式チャンネル)で情報発信中。メールマガジンはこちらから講読可能。
著作
- 生きる意味109:5万部のベストセラー
- 不安が消えるたったひとつの方法(KADOKAWA出版)
京都大学名誉教授・高知大学名誉教授の著作で引用、曹洞宗僧侶の著作でも言及。